Reproducibility in PyTorch: Myth or Reality?

Introduction #

I have an obsession with reproducibility! It is one of the main requirements of doing scientific work. Without it, the value of our work might be in danger. In different fields, various tools are used to ensure accuracy and consistency, and the same is true in our field—we rely on specific tools to build and validate our research. The frameworks we use for training and evaluation are among these tools

According to Papers with Code, framework usage distribution has shifted dramatically over time. The chart below shows the rise of PyTorch, now dominating the field. Therefore, here, I have decided to explore the reproducibility aspect of PyTorch.

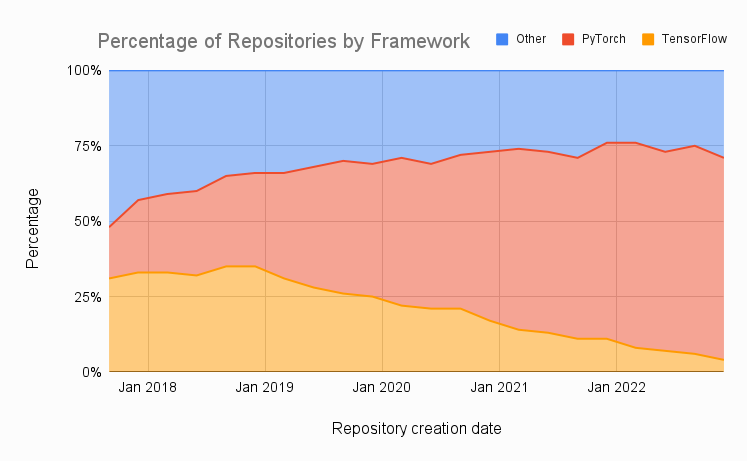
Figure 1: Framework usage distribution in machine learning research papers over time.

Interestingly! On PyTorch’s official website official website, it directly states:

Completely reproducible results are not guaranteed across PyTorch releases, individual commits, or different platforms. Furthermore, results may not be reproducible between CPU and GPU executions, even when using identical seeds.

So, while PyTorch is widely used, achieving perfect reproducibility is not feasible. In the following, I will try to shed light on some of the reasons.

Possible Reason #1: Floating-Point Non-Associativity #

Non-associative nature of floating-point arithmetic could be problematic here. Operations like summation can yield different results depending on the order of execution, and in parallel computing environments, this order is often non-deterministic. In deep learning, we often rely on GPUs that perform computations in parallel.

In deep learning, many core operations involve summation under the hood. For example, in the log-likelihood function, when we input a high-dimensional tensor and expect a single scalar output, the internal summation can lead to minor variations, introducing non-reproducibility. Similarly, matrix multiplication consists of numerous summation operations, many of which are executed in parallel across multiple threads. Since these operations are performed in different execution orders depending on the system’s workload and architecture, inconsistencies may arise whenever the model is run. For example, with float32 precision, due to rounding errors, $((a + b) + c)$ can produce a different result than $(a + (b + c))$. Consider three numbers:

$$a = 1.0000001, b = 1.0000002, c = 1.0000003$$

When computed as $((a + b) + c)$, the result is 3.000001, while computing as $(a + (b + c))$ gives 3.0000005. To better understand this phenomenon, let’s examine a toy example illustrated in Figure 2. This diagram shows a simple linear regression with one input vector and one weight vector—the most fundamental building block of neural networks. In deep learning, the entire architecture consists of numerous matrix multiplications, each involving thousands or millions of these dot product operations happening simultaneously across parallel GPU threads.

In our example, we have an input vector [1.0000001, 2.0000002, 3.0000003, 4.0000004] and a weight vector [5.0000005, 6.0000006, 7.0000007, 8.0000008]. When computing their dot product, we first multiply the corresponding elements, resulting in [5.00000060000005, 12.0000024000012, 21.0000042000021, 32.0000064000032]. The final step requires summing these products. Here’s where GPU parallelism introduces non-determinism: depending on how the GPU schedules threads, the summation might follow different patterns. Figure 2 shows two possible execution paths:

GPU TYPE #1 (Left-to-right addition): The products are added sequentially from left to right, resulting in a final value of 70.000015 after rounding.
GPU TYPE #2 (Balanced tree addition): The products are added in a balanced tree pattern, resulting in a final value of 70.000014 after rounding.

Figure 2: Demonstration of floating-point non-associativity in GPU computation.

These discrepancies might seem negligible at first glance, but they can have significant implications in deep learning. Even mathematically equivalent operations may yield slightly different results when executed in parallel. To understand the source of these variations, we need to take a closer look at how floating-point arithmetic works under the hood.

What is Under the Hood: Why Floating-Point Math Is not Exact #

But why does this non-associativity occur in the first place? The answer lies in the hardware constraints of floating-point representation. In PyTorch, neural network computations typically use 32-bit floating-point numbers (float32), which have a fixed structure:

1 bit for sign
8 bits for exponent
23 bits for mantissa (significant digits)

This fixed-width format means we can only represent a limited set of numbers exactly. When we perform addition between two floating-point numbers with different magnitudes, the smaller number’s least significant bits may be lost during alignment. For example, when adding the first two products from our example:

5.00000060000005 + 12.0000024000012

The computer must first align the decimal points by adjusting the smaller number’s exponent to match the larger one. During this process, some precision in the smaller number may be lost because the mantissa can only store 23 bits of information. After alignment and addition, if the result requires more than 23 bits of precision, rounding must occur. This is why different addition orders produce different results:

In left-to-right addition, we first add 5.00000060000005 + 12.0000024000012, round the result, then add 21.0000042000021, round again, and finally add 32.0000064000032 with a final rounding.
In balanced tree addition, we add (5.00000060000005 + 12.0000024000012) and (21.0000042000021 + 32.0000064000032) separately, round both results, and then add these rounded results together with a final rounding.

Each rounding operation potentially discards different bits, leading to the different final values we observed (70.000015 vs 70.000014).

To understand how precision is lost in floating-point arithmetic, let’s examine the binary representation using IEEE-754 float32 format. When adding numbers with different magnitudes like 12.0000024 and 5.0000006, their exponents must be aligned first. The normalized binary representation of 12.0000024 is approximately 1.10000000001000000000011 × 2^3, while 5.0000006 is represented as 1.01000000000000000011001 × 2^2. Before addition can occur, the smaller number (5.0000006) must have its mantissa right-shifted to match the larger number’s exponent. After shifting, 5.0000006 becomes 0.10100000000000000001100 × 2^3. Notice that this shift causes the rightmost bit from the original mantissa to be pushed beyond the 23-bit mantissa limit, resulting in lost precision. When these aligned mantissas are added, the result must again be normalized and rounded to 23 bits, potentially discarding additional bits.

These tiny losses in floating-point precision might seem insignificant, but they can accumulate rapidly across the millions of operations in a deep learning model. Since the order of addition affects the result—even when the operations are mathematically equivalent—running the same computation in parallel on a GPU can produce different outcomes. Now imagine this happening across millions of parameters, with thousands of operations in every forward and backward pass. Over time, these subtle discrepancies can snowball, potentially leading to divergent model behaviors—even when the training data and initial conditions remain the same. This illustrates why, despite setting fixed random seeds, achieving perfect reproducibility in neural network training remains a challenge. The interplay between floating-point arithmetic limitations and the inherent parallelism of GPU computation introduces variations that are practically impossible to eliminate entirely.

Possible Reason #2: cuDNN Algorithm Selection and Kernel Non-Determinism #

Many deep learning operations rely on CUDA kernels and cuDNN optimizations that prioritize performance over strict determinism. As a result, the same operation can produce different outcomes across runs. The cuDNN library, which is widely used for accelerating convolution operations, dynamically selects among multiple algorithms based on input dimensions and internal benchmarking. This introduces two key challenges for reproducibility.

1. Algorithm selection varies with input shape.
When torch.backends.cudnn.benchmark = True, cuDNN runs internal benchmarks to choose the fastest algorithm for each input configuration. Even small changes in input shape—such as batch size—can cause cuDNN to switch algorithms between runs. This dynamic behavior improves performance but introduces variability in training results. Disabling benchmarking by setting benchmark = False can reduce this variability, but only when input shapes remain constant.

2. Some operations are inherently non-deterministic.
Even when algorithm selection is fixed, certain operations in PyTorch lack deterministic implementations. To enforce strict reproducibility, PyTorch provides torch.use_deterministic_algorithms(True), which limits execution to deterministic variants when available. However, this can lead to two issues: slower training due to limited algorithm choices, and runtime errors if a non-deterministic operation is encountered.

Examples of such operations include torch.bmm() with sparse tensors, torch.index_add_(), torch.scatter_add_(), and torch.nn.functional.interpolate(). These are non-deterministic due to factors like atomic updates, floating-point precision, and the execution order of GPU threads. In Graph Neural Networks (GNNs), for instance, scatter_add_() is commonly used for aggregating messages between nodes. Because this operation performs atomic updates, the result may vary slightly across runs, even with fixed seeds. Ensuring reproducibility in such cases may require moving computations to the CPU or using alternative aggregation strategies.

Mitigation Strategy: Maximizing Reproducibility in PyTorch #

Due to the factors discussed earlier—such as floating-point non-associativity, parallel execution, and cuDNN algorithm variability—achieving complete reproducibility in PyTorch remains a challenge. In addition to these, there may be other sources of non-determinism not covered here, such as library version mismatches, hardware differences, or OS-level scheduling behaviour.

That said, the following setup represents the best you can do to reduce variability within PyTorch’s current limitations. It controls the major sources of randomness, including CPU and GPU computations as well as cuDNN’s behavior. To maximize reproducibility, use the following configuration:

def set_seed(seed: int = 42): 
    random.seed(seed) 
    np.random.seed(seed) 
    torch.manual_seed(seed) 
    torch.cuda.manual_seed(seed) 
    torch.cuda.manual_seed_all(seed) 
    torch.backends.cudnn.deterministic = True 
    torch.backends.cudnn.benchmark = False

Example: Graph Neural Network Non-determinism #

import torch
import torch_geometric
from torch_geometric.nn import GCNConv
import networkx as nx

# Set seeds for reproducibility
torch.manual_seed(42)
torch.cuda.manual_seed(42)

# Create a random graph
g = nx.erdos_renyi_graph(1000, 0.01)
edge_list = list(g.edges())
edge_index = torch.tensor(edge_list).t().contiguous()
edge_index = torch.cat([edge_index, edge_index.flip(0)], dim=1).to("cuda")

# Random node features
x = torch.rand(1000, 64, device="cuda")

# GCN layer that uses scatter operations internally
conv = GCNConv(64, 32).to("cuda")

# Run multiple times and collect results
results = []
for i in range(5):
    output = conv(x, edge_index)
    results.append(output.sum().item())

print(results)
print(f"All equal: {all(r == results[0] for r in results)}")

Here is the result produced by executing the above code:

[-259.5872802734375, -259.5871887207031, -259.5872802734375, -259.5872497558594, -259.5872802734375]
All equal: False

GNNs struggle with reproducibility because of how they update node features in parallel. Imagine 1000 people (nodes) passing messages to their friends at the same time. On a GPU, these messages are delivered simultaneously by many workers. Now, if several friends try to update the same person’s information at once, the exact order of those updates becomes unpredictable.

Technically, this happens because GCNs use scatter_add_()—a GPU operation that performs atomic updates. Atomic operations prevent memory conflicts when multiple threads access the same location, but they do not enforce a fixed order of execution. So, when node 5 and node 8 both try to update node 3’s features, the GPU can not guarantee which update is applied first. It is like two people trying to write on the same whiteboard at the same time—the final result depends on who finishes last.

Let’s look at a simple example. Suppose node A receives values 0.5 from node B and 0.3 from node C:

Run 1: B’s message is applied first, then C’s → total is 0.8
Run 2: C’s message is applied first, then B’s → ideally still 0.8
But due to floating-point rounding, these operations may yield slightly different results—like 0.80000007 vs. 0.79999995

Even though addition should give the same result no matter the order, computers do not always handle it exactly the same way—especially when using GPUs. Tiny differences can appear because of how numbers are stored and added. When this happens millions of times during training, it can change the final result of the model. This is because many updates happen at the same time, and the order of these updates can change each time you run the program. So, even if you fix the random seed and keep everything else the same, you might still get slightly different results. That is why getting exactly the same output every time is very difficult in practice.

Note: Want to explore more examples like this? Check out the following repository https://github.com/ameskandari/reproducibility-in-pytorch.

References #

[1] PyTorch Team. (2024). Randomness in PyTorch. PyTorch. Retrieved March 29, 2025, from https://pytorch.org/docs/stable/notes/randomness.html

[2] Papers with Code. (2023). Frameworks usage over time. Retrieved March 29, 2025, from https://paperswithcode.com/trends

[3] Elliott, J., Ivanov, I., & Hoefler, T. (2024). Impacts of floating-point non-associativity on reproducibility for HPC and deep learning applications (arXiv:2408.05148). arXiv. https://arxiv.org/abs/2408.05148

[4] Fey, M., & Lenssen, J. E. (2019). Fast graph representation learning with PyTorch Geometric (arXiv:1903.02428). arXiv. https://arxiv.org/abs/1903.02428

[5] NVIDIA. (2024). cuDNN Developer Guide. NVIDIA Developer Documentation. Retrieved March 29, 2025, from https://docs.nvidia.com/deeplearning/cudnn

[6] IEEE. (2019). IEEE Standard for Floating-Point Arithmetic (IEEE 754-2019). IEEE. https://ieeexplore.ieee.org/document/8766229

[7] Pineau, J., Vincent-Lamarre, P., Sinha, K., Larivière, V., Beygelzimer, A., d’Alché-Buc, F., … & Harchaoui, Z. (2021). Improving reproducibility in machine learning research (arXiv:2003.12206). arXiv. https://arxiv.org/abs/2003.12206

[8] Paszke, A., et al. (2019). PyTorch: An Imperative Style, High-Performance Deep Learning Library. https://arxiv.org/pdf/1912.01703

Bibtex #

@misc{eskandari2025pytorch,
  author       = {Eskandari, Amir},
  title        = {Reproducibility in PyTorch: Myth or Reality?},
  year         = {2025},
  howpublished = {\url{https://ameskandari.github.io/blog-main/posts/reproducibility-in-pytorch/}},
  note         = {Accessed: 2025-03-29. Licensed under the MIT License}
}